Deep learning (DL) revolutionised computer vision (CV) and artificial intelligence in general. It was a huge breakthrough (circa 2012) that allowed AI to blast into the headlines and into our lives like never before. ChatGPT, DALL-E 2, autonomous cars, etc. – deep learning is the engine driving these stories. DL is so good, that it has reached a point where every solution to a problem involving AI is now most probably being solved using it. Just take a look at any academic conference/workshop and scan through the presented publications. All of them, no matter who, what, where or when, present their solutions with DL.
The solutions that DL is solving are complex. Hence, necessarily, DL is a complex topic. It’s not easy to come to grips with what is happening under the hood of these applications. Trust me, there’s heavy statistics and mathematics being utilised that we take for granted.
In this post I thought I’d try to explain how DL works. I want this to be a “Deep Learning for Dummies” kind of article. I’m going to assume that you have a high school background in mathematics and nothing more. (So, if you’re a seasoned computer scientist, this post is not for you – next time!)
Let’s start with a simple equation:
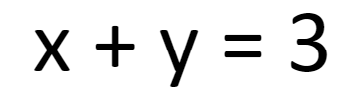
What are the values of x and y? Well, going back to high school mathematics, you would know that x and y can take an infinite number of values. To get one specific solution for x and y together we need more information. So, let’s add some more information to our first equation by providing another one:
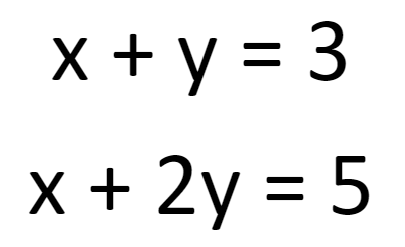
Ah! Now we’re talking. A quick subtraction here, a little substitution there, and we will get the following solution:
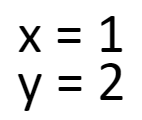
Solved!
More information (more data) gives us more understanding.
Now, let’s rewrite the first equation a little to provide an oversimplified definition of a car. We can think of it as a definition we can use to look for cars in images:
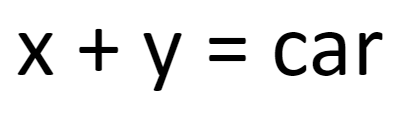
We’re stuck with the same dilemma, aren’t we? One possible solution is this:
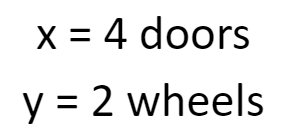
But there are many, many others.
In fairness, however, that equation is much too simple for reality. Cars are complicated objects. How many variables should a definition have to visually describe a car, then? One would need to take colour, shape, orientation of the car, makes, brands, etc. into consideration. On top of that we have different weather scenarios to keep in mind (e.g. a car will look different in an image when it’s raining compared to when it’s sunny – everything looks different in inclement weather!). And then there’s also lighting conditions to consider too. Cars look different at night then in the daytime.
We’re talking about millions and millions of variables! That is what is needed to accurately define a car for a machine to use. So, we would need something like this, where the number of variables would go on and on and on, ad nauseam:
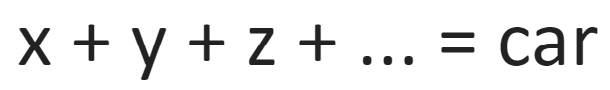
This is what a neural network sets up. Exactly equations like this with millions and millions and sometimes billions or trillions of variables. Here’s a picture of a small neural network (inicidentally, these networks are called neural networks because they’re inspired by how neurons are interconnected in our brains):
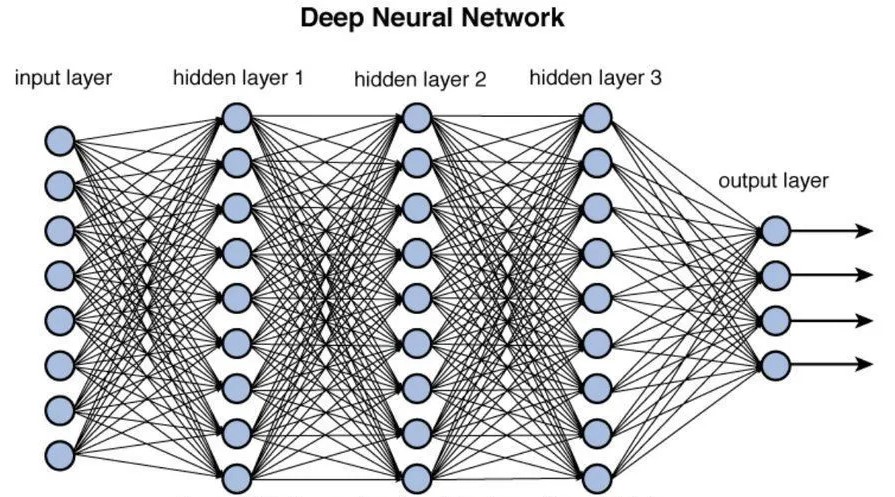
Each of the circles in the image is a neuron. Neurons are interconnected and arranged in layers, as can be seen above. Each neuron connection (the black lines above) has a weight associated with it. When a signal passes from one neuron to the next via a connection, the weight specifies how strong the original signal is going to be before it reaches the end of the connection. A weight can be thought of as a single variable – except that in technical terms, these variables are called “parameters“, which is what I’m going to call them from now on in this post.
The network above has a few hundred parameters (basically, the number of connections). To use our example of the car from earlier, that’s not going to be enough for us to adequately define a car. We need more parameters. Reality is much too complex for us to handle with just a handful of unknowns. Hence why some of the latest image recognition DL networks have parameter numbers in the billions. That means layers, and layers, and layers of neurons as well as all their connections.
(Note: a parameter count of a neural network will also include what’s called “biases” but I’ll leave that out in this post to keep things simple)
Now, initially when a neural network is set up with all these parameters, these parameters (variables) are “empty”, i.e. they have not been initiated to anything meaningful. The neural network is unusable – it is “blank”.
In other words, with our equation from earlier, we have to work out what each x, y, z, … is in the definitions we wish to solve for.
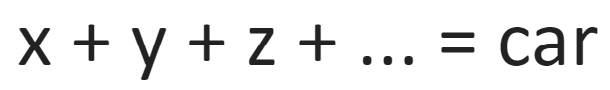
To do this, we need more information, don’t we? Just like in the very first example of this post. We don’t know what x, y, and z (and so on) are unless we get more data.
This is where the idea of “training a neural network” or “training a model” comes in. We throw images of cars at the neural network and get it to work out for itself what all the unknowns are in the equations we have set up. Because there are so many parameters, we need lots and lots and lots of information/data – cf. big data.

And so we get the whole notion of why data is worth so much nowadays. DL has given us the ability to process large amounts of data (with tonnes of parameters), to make sense of it, to make predictions from it, to gain new insight from it, to make insightful decisions from it. Prior to the big data revolution, nobody collected so much data because we didn’t know what to do with it. Now we do.
One more thing to add to all this: the more parameters in a neural network, the more complex equations/tasks it can solve. It makes sense, doesn’t it? This is why AI is getting better and better. People are building larger and larger networks (GPT-4 is reported to have parameters in the trillions, GPT-3 has 175 billion, GPT-2 has 1.5 billion) and training them on swathes of data. The problem is that there’s a limit to just how big we can go (as I discuss in this post and then this one) but this is a discussion for another time.
To conclude, this ladies and gentlemen are the very basics of Deep Learning and why it has been such a disruptive technology. We are able to set up these equations with millions/billions/trillions of parameters and get machines to work out what each of these parameters should be set to. We define what we wish to solve for (e.g. cars in images) and the machine works the rest out for us as long as we provide it with enough data. And so AI is able to solve more and more complex problems in our world and do mind-blowing things.
To be informed when new content like this is posted, subscribe to the mailing list (or subscribe to my YouTube channel!):